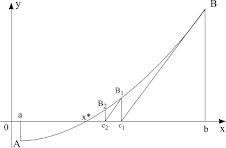
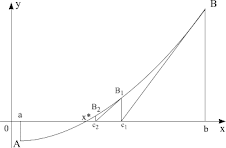
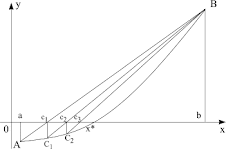
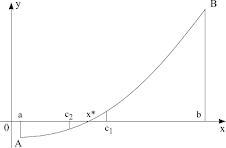
Ideea generală a metodei este următoarea: prin punctul (b,f(b)) se duce o dreaptă tangentă la graficul functiei . Se determină punctul c în care ea intersectează axa 0X. Acest punct se considera noua extremitate, prin care se duce tangenta. Procesul se repetă, până nu obţinem o apropiere suficientă de soluţia exactă. Pentru această metodă vom cere suplimentar, existenţa şi semnul constant al derivatei de ordin 2 pentru funcţia f(x) pe tot segmentul [a,b]. (pe segmentul dat funcţia să fie sau concavă sau convexă
Pentru a determina extremitatea din care pornim, trebuie să ţinem cont de următoarele cazuri posibile:
1) f’(x) > 0 f’’(x) > 0 2) f’(x) > 0 f’’(x) < 0
3) f’(x) < 0 f’’(x) > 0 4) f’(x) < 0 f’’(x) < 0
Este adevărată afirmaţia: Selectarea în calitate de punct iniţial al metodei tangentelor a extremităţii, pentru care se îndeplineşte relaţia f(x)*f’’(x) > 0 permite determinarea soluţiei cu orice grad de exactitate e
Vom cerceta cazul 1 – funcţia este convexă, crescătoare. (Celelalte cazuri se cercetează la fel)
Deoarece a doua derivată e mai mare ca 0, graficul funcţiei este superior coardei. Pornind din extremitatea în care funcţia este pozitivă vom obţine intersecţia cu axa 0x într-un punct interior al [a,b] Vom considera acest punct noua extremitate a intervalului. Repetând procedura vom obţine un şir de puncte interioare, care tind spre soluţia exactă. Dacă însă vom fixa extremitatea negativă, tangenta generată poate părăsi segmentul [a,b].
Deoarece funcţia este crescătoare, vom fixa extremitatea B
Teoremă
Dacă f(a)*f(b )<0, f’(x) şi f’’(x) 0 şi îşi păstrează semnul pe [a, b], atunci, pornind de lo o aproximare iniţială x0 [a, b] (f(x0)f’’(x0) > 0) soluţia unică a ecuaţiei pe [a, b] poate fi calculată cu orice grad de exactitate .
Demonstraţie: fie f(a) < 0, f(b) >0, f’(x) > 0 f’’(x) > 0. considerăm x0 = b, f(x0)>0. Pentru demonstrare vom folosi metoda inducţiei matematice, verificând ipoteza, cum că toate valorile şirului xn sunt > , n.
n = 0. x0 = b, f(x0)>0. evident.
Fie, pentru un careva n ipoteza este adevărată, xn > , Considerăm = xn + ( - xn), apoi aplicăm formula Tailor (pentru descompunerea funcţiei în sumă de polinoame) şi obţinem:
0 = f() = f(xn) + f’(xn) ( - xn) +1/2 f’’(cn) ( - xn)2 unde
Deoarece f’’(x) > 0, rezultă f(xn) + f’(xn) ( - xn) < 0 sau f’(xn) ( - xn) < - f(xn) ( - xn) < - f(xn)/ f’(xn)
< xn - f(xn)/ f’(xn) = xn+1. ,
Din formula recurentă rezultă direct că x0 > x1 > … >xn …> 1 - limita xn.
Trecând la limită obţinem
1 = 1 – f(1)/ f’(1), de unde f(1) =0 deci 1 = ceea ce şi trebuia de demonstrat.
Algoritmizarea metodei
0. Calculăm semnul derivatei 2 pe segmentul [a,b].
1. Fixăm punctul iniţial x0 conform formulei: f(x0)*f’’(x0)>0
2. Calculăm următoarea aproximaţie conform formulei:

3. Repetăm pasul 2 până nu obţinem soluţia cu exactitatea cerută.
Estimarea erorii.
Faptul că şirul aproximărilor succesive prin metoda tangentelor converge către soluţia exactă implică următoarea concluzie: cu cât mai multe iteraţii ale metodei vor fi realizate, cu atât mai bine va fi aproximată soluţia. Totuşi, am putea determina o formulă, care permite estimarea exactă a erorii de calcul, şi, prin urmare, exactitatea soluţiei obţinute.
Vom considera, că prima derivată a funcţiei f(x) este continuă pe segmentul [a,b].
Fie atunci m1 şi M1 două numere pozitive, pentru care are loc relaţia
0 < m1 | f’(x) | M1 < +

(exprimăm xn prin xn-1, ţinând cont de faptul că 0 = f(), îl adăugăm în partea stângă a egalităţii, apoi estimăm diferenţa între soluţia exactă şi cea aproximativă.
Pentru a deduce formula finală vom folosi
Teorema Lagrange Fie f:[a,b] R, continuă şi derivabilă pe [a,b] . Atunci c(a, b) astfel încât:
f(b) –f(a) = (b -a) f’(c)
fără demonstraţie

Deci dacă e necesar să obţinem soluţia cu exactitate dată , vom repeta aproximările până la obţinerea inegalităţii
Aici xn şi xn+1 sunt două aproximaţii succesive iar M1 şi m1 corespunzător marginea superioară şi inferioară a f’(x) pe [a, b].