METODA BISECŢEI

Fie dată ecuaţia f(x) = 0 (1)

Vom considera cazul, când funcţia este continuă pe [a,b] şi f(a)*f(b) < 0. Suplimentar vom considera că pe [a,b] semnul derivatei 1 a funcţiei este constant, deci avem doar o singură soluţie.
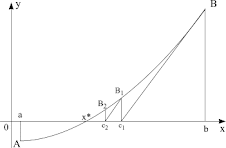
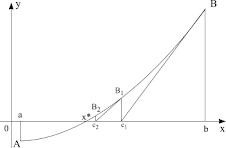
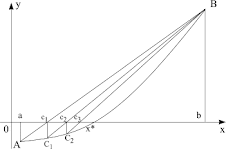
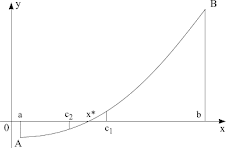
Pentru determinarea soluţiei ecuaţiei (1) vom detecta mijlocul segmentului [a,b],  = (a+b)/2, şi vom calcula valoarea funcţiei în acest punct. Dacă f() = 0, atunci  este soluţia ecuaţiei. În caz contrar cercetăm segmentele [a, ] şi [, b].
Pentru aproximarea următoare vom selecta acel segment, pentru care valoarea funcţiei în extremităţi are semne opuse. Dacă sign(f(a)) = sign(f()), atunci vom continua cercetarea pe segmentul [a1, b1], unde a1 , b1b . În caz contrar extremităţile vor fi a1a, b1. Noul segment [a1, b1] iarăşi se divizează, apoi se repetă cercetarea semnelor valorilor funcţiei în extremităţi şi în mijlocul segmentului. Procedura se repetă până când nu se obţine soluţia exactă sau (în majoritatea absolută a cazurilor!) devierea soluţiei aproximative de la cea exactă nu devine suficient de mică.

În procesul de construcţie a segmentelor succesive obţinem consecutivitatea segmentelor
[a,b], [a1, b1], [a2, b2], [a3, b3], ... [an, bn]...

Pentru fiecare din ele are loc relaţia f(ai)*f(bi) < 0 , i=1,...,n... (2)
Deoarece lungimea fiecărui segment următor este egală cu ½ din lungimea celui precedent putem exprima lungimea oricărui segment prin cea a segmentului iniţial:

bi - ai = (½ )i * (b – a) (3)

Din construcţie şi proprietăţile funcţiei f(x), rezultă că şirul extremităţilor stângi a, a1, a2, ..., an , ... este monoton crescător, mărginit superior, iar şirul extremităţilor drepte b, b1, b2, ..., bn , ... este monoton descrescător, mărginit inferior. De aici rezultă convergenţa ambelor şiruri şi existenţa limitei pentru fiecare din ele.

Trecând la limită în egalitatea (3) obţinem:

Trecând la limită în inegalitatea (2) din continuitatea f(x) primim ( f())2  0. Prin urmare f()=0 deci  e soluţia ecuaţiei (1).

Deoarece  e un punct din segmentul [an, bn] rezultă

0   - an  1/2n(b - a)


În cazul când semnul derivatei întâi alternează pe segmentul [a, b] , adică rădăcinile ecuaţiei nu sunt separate, metoda permite determinarea doar a unei soluţii.



ALGORITMIZAREA METODEI.

Datorită simplităţii sale metoda este uşor de realizat în formă algoritmică:
0. Ecuaţia se aduce la forma y=f(x) (pentru o prezentare mai comodă în formă de funcţie în interiorul programului)

1. Se introduc valorile a, b – extremităţile segmentului şi e – exactitatea cu care trebuie obţinută soluţia
2. Se calculează c=(a+b)/2, f(a), f(b), f(c).
3. Dacă sign( f(a)) = sign( f(c)), atunci vom considera că a trece în c. În caz contrar
(sign( f(b) ) = sign( f(c) )) b va primi valoarea lui c.
4. Pentru noile valori a şi b repetăm paşii 2 –3 atât timp cât (b - a)  e
5. Afişăm în calitate de soluţie mijlocul ultimului segment [a,b].